728x90
반응형
1. 알고리즘 복잡도 표현방법
1-1. 알고리즘 복잡도 계산이 필요한 이유
하나의 문제를 푸는 알고리즘은 다양함
* 정수의 절대값을 구하는 방법
* 방법1 : 값이 음수인지 확인해서 0보다 작은 음수일 때 -1을 곱하기
* 방법2 : 정수값을 재곱한 값에 루트를 씌우기디양한 알고리즘 중 어떤 알고리즘이 더 좋은지 분석하기 위해 복잡도를 정의하고 계산함
1-2. 알고리즘 복잡도 계산 항목
- 공간 복잡도 : 알고리즘이 사용하는 메모리 사이즈
- 시간 복잡도 : 알고리즘 실행 속도
1-3. 알고리즘 성능 표기법
- 오메가 표기법
- 알고리즘 최상의 실행 시간을 표기
- 세타 표기법
- 알고리즘 평균 실행시간을 표기
- 빅오 표기법
- 최악의 실행 시간을 표기
- 아무리 최악의 상황이라도 이 정도의 성능은 보장함을 의미
- 가장 많이 사용
1-4 빅오 표기법
- 입력 n에 따라 결정되는 시간 복잡도 함수
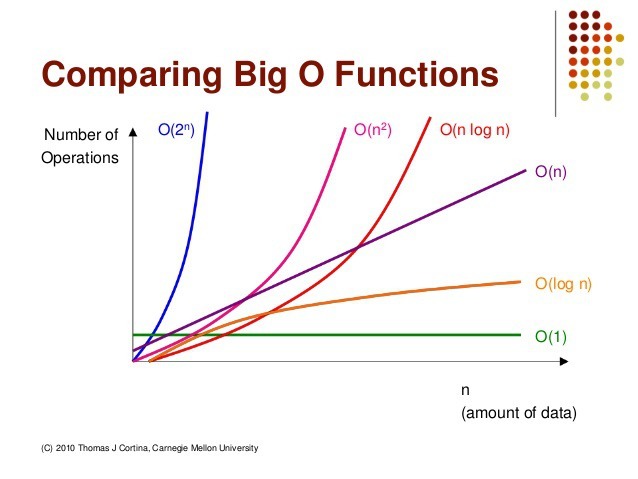
- O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(2n) < O(n!)
- 입력 n에 따라 시간 복잡도가 늘어날 수 있음
2. 공간 복잡도
- 공간 복잡도(Space Complexity) 작성한 프로그램이 얼마나 많은 공간(메모리)을 차지하느냐를 분석하는 방법
- 컴퓨터 성능의 발달로 인해 메모리 공간이 넘쳐나다 보니 중요도가 떨어짐
- 공간 복잡도를 결정하는 것은 배열의 크기가 몇인지, 얼마 만큼의 동적 할당인지, 몇 번의 호출을 하는 재귀함수가 있는지가 영향을 끼침
- 알고리즘은 시간 복잡도가 중
3, 시간 복잡도
- 특정 알고리즘이 어떤 문제를 해결하는데 걸리는 시간을 의미
- 같은 결과를 갖는 프로그래밍 소스도 작성 방법에 따라 걸리는 시간이 달라지며 시간이 적게 걸리는 소스가 좋은 소스
3-1. 0(1)
- 입력 데이터의 크기와 상관없이 언제나 일정한 시간이 걸리는 알고히즘을 나타냄. 데이터가 얼마나 증가하든 성능에 영향을 미치지 않음
def print_data(data): print(data[0])
3-2. O(logn)
- 입력 데이터의 크기가 커질수록 처리 시간이 로그 만큼 짧아지는 알고리즘. 이진 탐색이 대표적이며 재귀가 순기능으로 이루어지는 경우도 해당됨
def print_data(data): i = data while i > 1: print(i) i = i / 2
3-3. O(n)
- 선형 복잡도라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미(반복)
def print_data(data): for i in range(len(data)): print(data[i])
3-4. O(n2)
- 2차 복잡도라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미
def print_data(data): for i in range(len(dataa)): for j in range(len(data)): print(data[i], data[j])
4. 실제 알고리즘을 예로 알고리즘 시간 복잡도와 빅오 표기법 알아보기
- 1부터 n까지의 합을 구하는 알고리즘

반응형
'Python > 알고리즘&자료구조' 카테고리의 다른 글
| Python 자료구조 & 알고리즘 - 재귀호출 (0) | 2023.02.21 |
|---|---|
| Python 자료구조 & 알고리즘 - 정렬(버블, 삽입, 선택) (0) | 2023.02.21 |
| Python 자료구조&알고리즘 - 힙(Heap) (0) | 2023.02.01 |
| Python 자료구조&알고리즘 - 트리(Tree), 이진 탐색 (0) | 2023.01.31 |
| Python 자료구조&알고리즘 - 해쉬 테이블(Hash Table) (0) | 2023.01.30 |