728x90
반응형
1. 트리(Tree)
- Node와 Branch를 이용해서 사이클을 이루지 않도록 구성한 데이터 구조
- 트리중 이진 트리(Binary Tree)형태의 구조로 탐색(검색)알고리즘을 구현을 위해 많이 사용됨
2. 알아둘 용어
- Node: 트리에서 데이터를 저장하는 기본 요소(데이터와 다른 연결된 노드에 대한 Branch 정보를 포함)
- Root Node: 트리 맨 위에 있는 노드
- Level: 최상위 노드를 Level 0으로 했을 때 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node: 어떤 노드의 상위 레벨에 연결된 노드
- Child Node: 어떤 노드의 하위 레벨에 연결된 노드
- Leaf Node: Child Node가 하나도 없는 노드
- Sibling Node: 동일한 Parent Node를 가진 노드
3. 이진 트리와 이진 탐색 트리(Binary Search Tree)
- 이진 트리: 노드의 최대 Branch가 2개인 트리
- 이진 탐색 트리(Binary Search Tree,BST) 이진 트리에 추가적인 조건이 있는 트리
- 왼쪽 노드는 해당 노드보다 작은 값이며, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있다

4. 자료 구조 이진 탐색 트리의 장점과 주요 용도
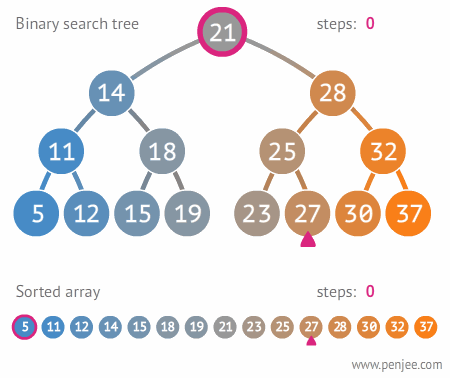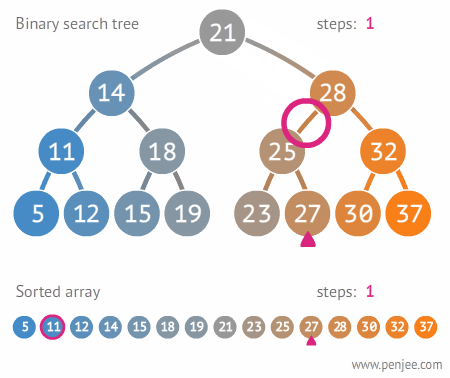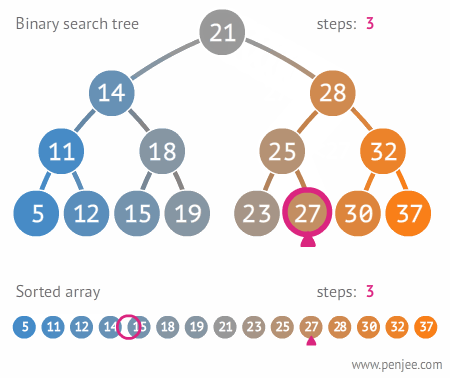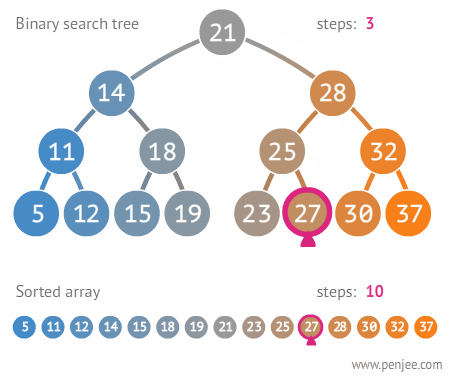
- 주요 용도: 데이터 검색(탐색)
- 장점: 탐색 속도를 개선할 수 있음
- 단저: 이진 탐색 트리 알고리즘 이해 후에 살펴봐야 함
5. 파이썬 객체지향 프로그래밍으로 이진 탐색 트리 구현하기
5-1. 노드 클래스 만들기
[ ]
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
5-2. 이진 탐색 트리에 데이터 넣기
- 조건: 중복 데이터를 넣지 않음
[ ]
class NodeMgmt:
def __init__(self, head):
self.head = head # head에 head값 저장
def insert(self, value):
self.current_node = self.head # current_node에 head 저장
while True:
if value < self.current_node.value: # value값이 current_node의 값보다 작으면
if self.current_node.left != None: #
self.current_node = self.current_node.left # current_node에 current_node.left 저장
else:
self.current_node.left = Node(value) # current_node.left에 값이 없으면 value값 저장
break
else:
if self.current_node.right != None:
self.current_node = self.current_node.right
else:
self.current_node.right = Node(value)
break
[ ]
head = Node(10)
BST = NodeMgmt(head)
[ ]
BST.insert(5)
[ ]
class NodeMgmt:
def __init__(self, head):
self.head = head # head에 head값 저장
def insert(self, value):
self.current_node = self.head # current_node에 head 저장
while True:
if value < self.current_node.value: # value값이 current_node의 값보다 작으면
if self.current_node.left != None: #
self.current_node = self.current_node.left # current_node에 current_node.left 저장
else:
self.current_node.left = Node(value) # current_node.left에 값이 없으면 value값 저장
break
else:
if self.current_node.right != None:
self.current_node = self.current_node.right
else:
self.current_node.right = Node(value)
break
def search(self, value):
self.current_node = self.head
while self.current_node:
if self.current_node.value == value:
return True
elif value < self.current_node.value:
self.current_node = self.current_node.left
else:
self.current_node = self.current_node.right
return False
[ ]
head = Node(10)
BST = NodeMgmt(head)
BST.insert(2)
BST.insert(5)
BST.insert(13)
BST.insert(19)
BST.insert(11)
BST.insert(8)
[ ]
BST.search(11)
True [ ]
BST.search(7)
False5-4. 이진 탐색 트리의 삭제
- Leaf Node 삭제
- Leaf Node: child Node가 없는 Node
- 삭제할 Node의 Parent Node가 Node를 가리키지 않도록 함
- 삭제할 node 탐색하기
searched = False
self.current_node = self.head
self.parent = self.head
while self.current_node:
if self.current_node.value == value
searched = True
break
elif value < self.current_node.value:
self.parent = self.current_node
self.current_node = self.current_node
self.current_node = self.current_node.left
else:
self.parent = self.current_node
self.current_node = self.current_node.right
if searched == Fase:
return False- 삭제할 node가 Leaf Node인 경우
if self.current_node.left == None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = None
else:
self.parent.right = None- Child Node가 하나면 node를 삭제
- 삭제할 node의 Parent Node가 삭제할 Node의 Child Node를 가리키게 함
if self.current_node.left != None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = self.current_node.left
else:
self.parent.right = self.current_node.left
elif self.current_node.left == None and self.current_node.right != None:
if value > self.parent.value:
self.parent.left = self.current_node.right
else:
self.parent.right = self.current_node.right- Child Node가 두개인 Node를 삭제
- 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 함
- 삭제할 Node가 Parent Node 왼쪽에 있을 때
- 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 없을 때
- 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 있을 때
- 삭제할 Node가 Parent Node 오른쪽에 있을 때
- 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 없을 때
- 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 있을 때
가장 작은 값을 가진 Node의 Child Node가 왼쪽에 있을 경우는 절대 없음! 왼쪽 Node가 있다는 것은 해당 Node보다 더 작은 값을 가진 Node가 존재한다는 뜻이기 때문
- Child Node가 두개인 Node를 삭제하는 코드 구현하기
- 삭제할 Node의 오른쪽 자식을 선택
- 오른쪽 자식의 가장 왼쪽에 있는 Node를 선택
- 해당 Node를 삭제할 Node의 Parent Node의 왼쪽 Branch가 가리키게 함
- 해당 Node의 왼쪽 Branch가 삭제할 Node의 왼쪽 Child Node를 가리키게 함
- 해당 Node의 오른쪽 Branch가 삭제할 Node의 오른쪽 Child Node를 가리키게 함
- 만약 해당 Node가 오른쪽 Child Node를 가지고 있었을 경우, 해당 Node의 본래 Parent Node의 왼쪽 Branch가 해당 오른쪽 Child Node를 가리키게 함
if self.current_node.left != None and self.current_node.right != None:
if value < self.parent.value:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.left = self.change_node
self.change_node.right = self.current_node.right
self.change_node.left = self.current_node.left
else:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.right = self.change_node
self.change_node.right = self.current_node.right
self.change_node.left = self.current_node.left
return True5-5 전체 코드 구현
[ ]
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
[ ]
class NodeMgmt:
def __init__(self, head):
self.head = head
def insert(self, value):
self.current_node = self.head
while True:
if value < self.current_node.value:
if self.current_node.left != None:
self.current_node = self.current_node.left
else:
self.current_node.left = Node(value)
break
else:
if self.current_node.right != None:
self.current_node = self.current_node.right
else:
self.current_node.right = Node(value)
break
def search(self, value):
self.current_node = self.head
while self.current_node:
if self.current_node.value == value:
return True
elif value < self.current_node.value:
self.current_node = self.current_node.left
else:
self.current_node = self.current_node.right
return False
def delete(self, value):
searched = False
self.current_node = self.head
self.parent = self.head
while self.current_node:
if self.current_node.value == value:
searched = True
break
elif value < self.current_node.value:
self.parent = self.current_node
self.current_node = self.current_node.left
else:
self.parent = self.current_node
self.current_node = self.current_node.right
if searched == False:
return False
# 삭제할 노드가 leaf node인 경우
if self.current_node.left == None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = None
else:
self.parent.right = None
# 삭제할 노드의 child node가 하나인 경우
if self.current_node.left != None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = self.current_node.left
else:
self.parent.right = self.current_node.left
elif self.current_node.left == None and self.current_node.right != None:
if value < self.parent.value:
self.parent.left = self.current_node.right
else:
self.parent.right = self.current_node.right
# 삭제할 노드의 child node가 두개인 경우
if self.current_node.left != None and self.current_node.right != None:
if value < self.parent.value:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.left = self.change_node
self.change_node.right = self.current_node.right
self.change_node.left = self.current_node.left
else:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.right = self.change_node
self.change_node.right = self.current_node.right
self.change_node.left = self.current_node.left
return True
5-6 전체 코드 테스트
[ ]
# random 라이브러리
# random.randint(숫자1, 숫자2) : 숫자1부터 숫자 2사이에 있는 숫자를 랜덤하게 선택하여 리턴
import random
bst_nums = set()
while len(bst_nums) != 100:
val = random.randint(0, 999)
if val != 500:
bst_nums.add(val)
print(bst_nums)
{4, 9, 17, 20, 35, 40, 42, 563, 568, 578, 579, 75, 592, 80, 96, 100, 106, 107, 110, 628, 631, 632, 634, 138, 655, 152, 168, 170, 684, 174, 176, 182, 183, 185, 699, 702, 703, 190, 194, 209, 728, 735, 227, 229, 230, 231, 240, 757, 250, 763, 764, 765, 766, 770, 775, 272, 789, 793, 288, 290, 805, 812, 814, 821, 309, 826, 833, 834, 836, 324, 848, 343, 857, 346, 354, 359, 369, 883, 373, 376, 896, 901, 903, 395, 910, 398, 914, 916, 920, 412, 934, 423, 936, 955, 446, 968, 972, 977, 465, 480}
[ ]
# 루트노드를 500으로 설정, 100개의 데이터를 추가
head = Node(500)
binary_tree = NodeMgmt(head)
for num in bst_nums:
binary_tree.insert(num)
[ ]
# 데이터가 모두 잘 저장되었는지 탐색
for num in bst_nums:
if binary_tree.search(num) == False:
print('검색 실패 : ', num)
[ ]
delete_nums = set()
bst_nums = list(bst_nums)
while len(delete_nums) != 10:
delete_nums.add(bst_nums[random.randint(10,99)])
print(delete_nums)
{96, 376, 231, 240, 977, 465, 628, 728, 826, 190}
[ ]
for del_num in delete_nums:
if binary_tree.delete(del_num) == False:
print('삭제 실패', del_num)
else:
print('삭제 성공', del_num)
삭제 성공 96
삭제 성공 376
삭제 성공 231
삭제 성공 240
삭제 성공 977
삭제 성공 465
삭제 성공 628
삭제 성공 728
삭제 성공 826
삭제 성공 190
[ ]
False [ ]
True반응형
'Python > 알고리즘&자료구조' 카테고리의 다른 글
| Python 자료구조 & 알고리즘 - 복잡도 (0) | 2023.02.20 |
|---|---|
| Python 자료구조&알고리즘 - 힙(Heap) (0) | 2023.02.01 |
| Python 자료구조&알고리즘 - 해쉬 테이블(Hash Table) (0) | 2023.01.30 |
| Python 알고리즘&자료구조 더블 링크드 리스트(Doubly Linked List) (0) | 2023.01.29 |
| Python 자료구조&알고리즘 - 링크드리스트(Linked List) (0) | 2023.01.28 |